定理 1　三角形 ABC とその各頂点から対辺への垂線の上にない点 G があるとき,
G を通って AG, BG, CG のそれぞれに直交する直線と BC, CA, AB との交点は一直線上にある。

頂点 A, B, C と G はマウス
(タブレットならば指)で動かせます。

以下の説明にある垂心 H,
I, m を または します。
黄色い直線が m で,
黄色い円の中心は H で半径は
HA・HD = HB・HE = HC・HF の平方根です
(D, E, F はそれぞれ A, B, C から
対辺への垂線の足)。

　この定理は AG, BG, CG に直交する直線と BC, CA, AB との交点をそれぞれ P, Q, R とするとき,
BP/PC, CQ/QA, AR/RB を始点が G, 終点が A, B, C のベクトル どうしの内積で表し,
メネラウスの定理を使えば証明できます。
　⊿ABC の垂心を H とし, A, B, C から対辺への垂線の足をそれぞれ D, E, F とします。 また, 点 X に対してG を通って GX に直交する直線を G|X で表すことにします。
　定理の結論の直線を l(G) で表すことにします。 G が直線 AD 上にあっても A, H, D と異なれば, G|B, G|C はそれぞれ AC, AB と異なる点で交わります。 この 2点を通る直線も l(G) で表します。 G が BE, CF 上にあるときも同様とします。
　線分 XY を直径とする円を CRL(XY) で表すことにします。
　定理 2　G を A, B, C, D, E, F, H と異なる点とすれば, 以下の (1), (2), (3), (4) が成り立つ。
　(1) l(G) = AB となるための必要十分条件は G が CRL(AB) 上にあることである。 G が CRL(AB), CRL(BC), CRL(CA) のいずれの上にもなければ, l(G) は A, B, C を通らない。
　(2) ⊿ABC が鋭角三角形で l が A, B, C を通らない直線のとき, l(G) = l となる点 G は２つである。 これらを G₁, G₂ とするとき, H は線分 G₁G₂ 上にあって HG₁・HG₂= HA・HD が成り立つ (注: HA・HD = HB・HE = HC・HF)。
　(3) ⊿ABC が直角三角形で l が A, B, C を通らない直線のとき, l(G) = l となる点 G は 1 個または 0 個である。
　(4) ⊿ABC が鈍角三角形で l が A, B, C を通らない直線のとき, l(G) = l となる点 G は 2, 1, 0 個である。 2 個のとき, それらを G₁, G₂ とすれば, H を始点とする半直線上にあり, HG₁・HG₂ = HA・HD が成り立つ。 1 個のとき, それを G とすれば, HG² = HA・HD が成り立つ。
　　
　上の (1) は明らかです。 (2), (3), (4) も以下のことからわかります。
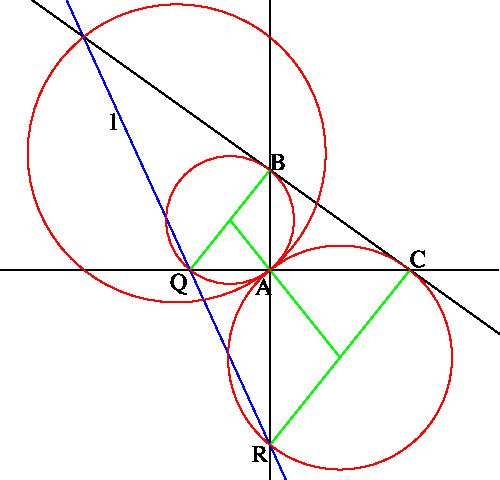
　l を A, B, C を通らない直線とし, BC, CA, AB との交点をそれぞれ P, Q, R とします。 l(G) = l となる点 G は CRL(AP), CRL(BQ), CRL(CR) の交点です。 ニュートンの定理より, 線分 AP, BQ, CR のそれぞれの中点は一直線上にあります。 この直線を m とすれば, CRL(AP), CRL(BQ), CRL(CR) は m に関して対称ですから, m に関して G と 対称な点 I に対しても l(I) = l となります。
　⊿ABC が鋭角三角形ならば, CRL(AP), CRL(BQ), CRL(CR) が 2点で交わることは容易にわかります。
　∠A が直角のときは CRL(AP), CRL(BQ), CRL(CR) は A で交わります。 これら３つの円が A で接するための必要十分条件は BQ と CR が平行になることです(上左図参照)。
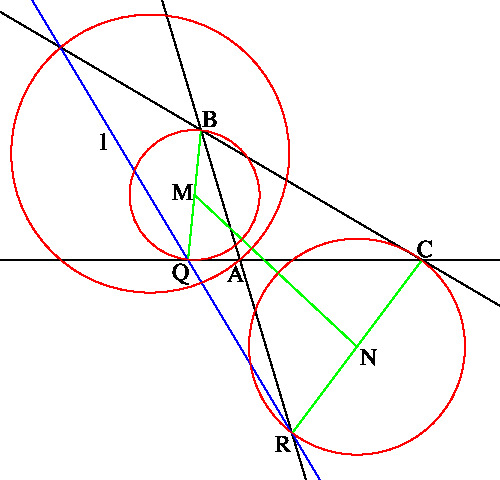
　⊿ABC を ∠A が鈍角の三角形であるとし, 線分 BQ, CR の中点をそれぞれ M, N とします。 CRL(AP), CRL(BQ), CRL(CR) は不等式 |BQ - CR| ≦ 2MN ≦ BQ + CR において二つの不等号が成り立てば 2点で交わり, いずれかの等号が成り立てば一点で接し, それ以外のときは交わりません(上右図参照)。
　⊿ABC は直角三角形ではないとし, G を l(G) = l となる点とします。 I を GH 上の点で HG・HI = HA・HD を満たすとします。 ∠ADP は直角ですから, D は CRL(AP) 上にあります。 したがって, 方べきの定理により, I は CRL(AP) 上にあります。 同様に CRL(BQ), CRL(CR) 上にもありますから, l(I) = l となります。